【音データのしくみ】音声信号処理の基礎知識シリーズその1

こんにちは。スキルアップAIの小宮です。
本ブログでは、AIを用いた音声・音楽モデルについて学ぶにあたって必要な、音声信号処理の基礎知識について解説します。第1回の今回は、まず音データのしくみについて解説します。

1.音データのしくみ

そもそも音はコンピュータ上でどのようにデータ化されているのでしょうか。
音の本質は空気の振動からなる信号、すなわち波です。波の波形を構成する要素は、大きく分けて振幅（音の大きさ）と周波数（音の高さ）の2つに分けられます。
振幅は量子化、周波数は標本化によってデジタル信号として記録することができます。そして音データはコンピュータ上ではデジタル信号として保存されます。

量子化

量子化とは、信号の大きさを離散的な値（デジタル値）で近似して表すことです。
大きさを表す際に用いるビットの数を量子化ビット数（ビット深度）と呼び、これが大きいほど振幅を細やかに表現できます。特に音声信号については、振幅を-1〜1の間の値に収まるように近似して表現します。またビット深度には、多くの場合16bit（65536段階）が用いられます。

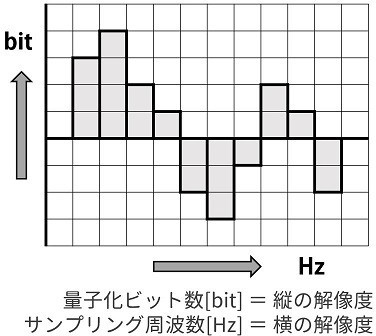
図1. 量子化ビット数とサンプリング周波数

標本化

標本化（サンプリング）とは、連続信号（アナログ信号）を⼀定の間隔を空けて測定し、離散信号（デジタル信号）として記録することです。測定する周期の逆数をサンプリング周波数（Sf）と呼び、Sf = Ｎ Hz のとき 1 秒間に N 回波形のサンプルを取ることを表します。

また Sf の半分の値をナイキスト周波数と呼びます。理論上、記録したい信号の周波数の2倍の Sf でサンプリングを行えば、出来上がったデジタル信号を補完することで元の波形を完全に復元することができます。これを標本化定理と呼びます。逆に言えば、ナイキスト周波数より高い周波数の信号は記録・復元できず、ノイズになってしまいます。
例として4 Hz の信号を Sf = 8 Hzで記録した場合を見てみましょう。

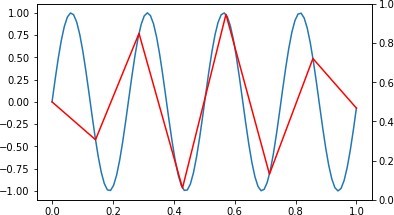
図2. Sf = 100 Hz で記録した場合（青）と Sf = 8 Hzで記録した場合（赤）

上図において、赤線がSf = 8 Hzで記録した場合であり、青線はSf = 100 Hzで記録した場合です。青線は、サンプリング周波数が十分に大きいため、元の信号を完全に捉えています。Sf = 8 Hzで記録した赤線は、一見すると元の信号とかけ離れているように見えますが、サンプリング後の信号を離散時間フーリエ変換し、さらに逆フーリエ変換を行うと元の信号を復元することができます。

これは、各サンプル点の値を掛けたsinc関数 = sin(πx)/πxを各点の位置に並べて、すべて足し合わせることに相当します。これにより私たちは音データを「音として聞く」ことができるわけです。

人間の聴覚の可聴域はおおよそ20 Hz〜20 kHzであるため、Sf を40 kHz 以上に設定すれば、理論上すべての音を表現することができます。実際、多くの音響機器において、標準の Sf は44.1 kHzまたは 48 kHzに設定されています。

ハイレゾについて

量子化ビット数・サンプリング周波数の高い音データを⼀般にハイレゾ（Hi-Resolution）音源と呼びます。例としては24 bit/96 kHzの音源などがあります。量子化ビット数と Sf を画像における縦横の解像度とみなせば、ハイレゾ音源は解像度の高い画像と似たようなものです。

人間の可聴域を考えると、Sf を44.1 kHz以上に設定する意味はないように思えます。しかし先述した標本化定理から、シンバルやハイハットなど、ナイキスト周波数を超える高さの音を録音すると、それがノイズとして記録されてしまうのです。ですがハイレゾ音源ならば、そのノイズを生じさせずに録音を行えるという利点があります。

2.まとめ

今回はデジタル信号としての音声波形について解説しました。音声信号処理では、音声波形そのものを操作することは少なく、主に周波数領域（音を周波数別に分解した状態）に変換してから操作します。
次回は音を周波数領域に変換するためのフーリエ変換について解説していきます。

3.おわりに

本ブログで紹介した音声信号処理には、Pythonが不可欠です。
スキルアップAIでは、「機械学習のためのPython入門講座」を開講中です。
本講座では、Pythonプログラミング未経験レベルから、scikit-learnを用いて機械学習モデルを構築できるようになることを目指します。 ぜひ受講をご検討ください。

また、毎週水曜日に実践的AI勉強会「スキルアップAIキャンプ」を開催しています。勉強会では、様々な実践的テーマを取り上げ、データ分析・AI開発の実務力アップにつながるヒントをご提供します。講師が参加者の皆さんからの質問や悩みに答えるコーナーもあります。
興味がある方はぜひ参加してみてください！

第2回「スペクトル解析」はこちら
音声信号処理の基礎知識シリーズの記事一覧はこちら

4.参考文献