因果推論の考え方と主な手法

こんにちは。スキルアップAIの深作です。私は現在、政治学についてのデータ分析の研究に取り組んでいます。今回はそのデータ分析で使っている「因果推論」という考え方について紹介したいと思います。この記事を通じて因果推論に対するイメージを掴んでいただけたら幸いです。

<目次>

「因果推論」とは
「統計的因果推論」とは
「統計的因果推論」で用いられる主な手法
おわりに
参考文献

1.「因果推論」とは

「2つのことがらのうち、どちらかが原因で、どちらかが結果である」状態を因果関係があるといいます[1]。そして、データに基づいて因果関係を推定することを因果推論といいます。なお、因果関係と相関係数は別の概念です。相関関係と因果関係の両方があるという場合もあれば、相関関係はあるが因果関係がないという場合もあります。

因果推論について具体的な例を挙げると、「店舗Aで広告を出したところ、売上が上がった。この売上が上がった原因は本当に広告なのか、それとも偶然であったり、別の要因なのではないか」を推定するといったことが考えられます。

久米ら[2]によると、ある2つの事象について因果関係があることを示したい場合、以下の3条件を満たす必要があります。

「原因の変化と結果の変化を同時に観測することができる（相関関係があること）」・・・①

「原因は結果に先行して起こる」・・・②

「他の変数原因と結果の変化を観測することができる」・・・③

この3つの条件のうちの③の条件を満たすことは、現実的には非常に困難です。なぜなら、「他の変数の影響が無い状況において、」という部分が現実に反しているからです。因果推論では、現実に反していることを反事実といいます。当然、反事実は観測されません。本当に知りたいことを観測できないということで、この問題は「因果推論の根本問題」と呼ばれています。[3]

2.「統計的因果推論」について

「因果推論の根本問題」に取り組む際には、通常、統計学が用いられます。このため、統計学を用いて因果推論を行うことを特に「統計的因果推論」といいます。

「統計的因果推論」では、基本的に、「特定の変数があるかどうか」以外の条件に違いがないとみなすことができるかどうかを統計学を用いて検証します。因果推論では、「特定の変数があるかどうか」以外の条件に違いがないことを同質であると表現します。

具体的な例を挙げます。「広告を出した店舗A」と「広告を出していない店舗B」があるとし、「広告の効果」を導きたいとします。そこで、この2店舗の差異が「広告を出したことだけ」といえるかどうかを統計学を用いて検証します。

上記の例では、店舗Aと店舗Bでは、立地条件などが異なるため、「特定の変数があるかどうか」以外の条件に違いがないことを示すことは困難です。このため実際には、いくつかのデータを集めて、平均的に差異がないかどうかを検証します。

前述した久米ら[2]の3条件のうち、①と③がこの反事実との比較によって立証する事ができます。

条件①については、広告を出した店舗Aでのみ売上が上がり、広告を出していない店舗Bでは売上が上がっていないことを確認します。

条件②については、広告を出した後の売上を比較することで原因が結果より先行していることを確認します。

条件③については、「広告を出したかどうか以外は同質の2グループ」を用意していることから、この条件を満たしているといえます。

「統計的因果推論」では、このように統計学を用いて、検証したい原因となる変数以外を同じとする2グループの比較を行い、因果関係を検証します。

3.「統計的因果推論」で用いられる主な手法

ここでは「統計的因果推論」にて主に用いられる手法として、「ランダム化比較試験」、「差分の差分法」、「回帰不連続デザイン」の3つを紹介します。

1つ目の「ランダム化比較試験」は最も一般的に想起される実験です。グループを無作為に2つに分けて、片方にだけ影響を与え（例：広告を打つ、投薬をする）、もう片方のグループには与えないようにします。このとき比較対象を無作為（ランダム）にグループに分けることで比較対象の差を平均します。「ランダム化比較試験」では、この差を統計学的に考察します。

2つ目の「差分の差分法」は元々あった差異を考慮し、その差異の変化を見る手法です。英語では「Difference in Differences」となるため、「DID法」と呼ばれることもあります。

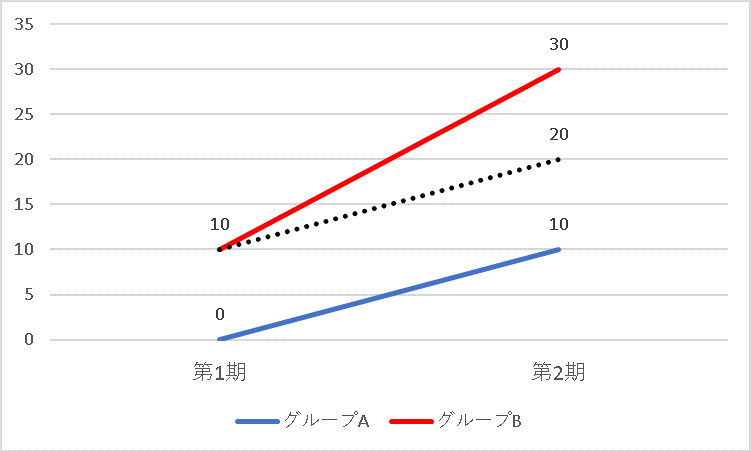
下記画像の例を考えます。グループ Aとグループ Bには最初10の差があり、グループ Aとグループ Bの差は、時間に応じて、同じように変化すると仮定します。（黒点線と青線）
この仮定に反し、実際にはグループ Bは赤線のように上昇しました。このとき、赤線と黒点線の差が今回の原因がもたらした結果となります。「差分の差分法」では、この差を統計学的に考察します。